Chapter 22. Elementary Graph Algorithms¶
This chapter discusses:
- Representing a graph
- Searching a graph
22.1 Representations of graphs¶
There are two standard ways to represent a graph G = (V, E):
- (A collection of) adjacency lists
- An adjacency matrix
Choices:
- The adjacency-list representation provides a compact way to represent sparse graphs (where |E| is much less than |V|2); it is usually the method of choice. Most of the graph algorithms presented in this book assume that an input graph is represented in adjacency-list form.
- The adjacency-matrix representation is preferred when the graph is dense (|E| is close to |V|2).
The following figure shows two representations of an undirected graph. (a) An undirected graph G with 5 vertices and 7 edges. (b) An adjacency-list representation of G. (c) The adjacency-matrix representation of G.
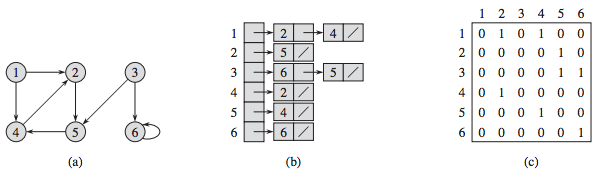
The following figure shows two representations of a directed graph. (a) A directed graph G with 6 vertices and 8 edges. (b) An adjacency-list representation of G. (c) The adjacency-matrix representation of G.
The adjacency-list representation of a graph G = (V, E) consists of an array Adj of |V| lists, one for each vertex in V . For each u ∈ V , the adjacency list Adj[u]" contains all the vertices v such that there is an edge (u, v) ∈ E. That is, Adj[u]" consists of all the vertices adjacent to u in G.
- If G is a directed graph, the sum of the lengths of all the adjacency lists is |E|, since an edge of the form (u, v) is represented by having v appear in Adj[u].
- If G is an undirected graph, the sum of the lengths of all the adjacency lists is 2|E|, , since if (u, v) is an undirected edge, then u appears in v's adjacency list and vice versa.
[p591]
A potential disadvantage of the adjacency-list representation is that it provides no quicker way to determine whether a given edge (u, v) is present in the graph than to search for v in the adjacency list Adj[u]. An adjacency-matrix representation of the graph remedies this disadvantage, but at the cost of using asymptotically more memory.
We can readily adapt adjacency lists to represent weighted graphs (graphs for which each edge has an associated weight), typically given by a weight function w. We simply store the weight w(u, v) of the edge (u, v) with vertex v in u’s adjacency list.
[p591-592]
Representing attributes¶
[p592]
For example, in an object-oriented programming language, vertex attributes might be represented as instance variables within a subclass of a Vertex class